2. XGboost 上:原理
2. XGboost 上:原理
1. XGboost 目标函数
XGboost的全称是eXtreme Gradient Boosting,它是经过优化的分布式梯度提升库,并且适合多平台和gpu计算。 XGBoost的目标函数由训练损失和正则项构成,定义如下:
其中,是训练损失, 是正则项。
这里,我们只要理解3个名词,1.训练损失,2. 所代表的的每颗树的函数表示, 3.每颗树的复杂度总和代表的正则项部分。
- 对于机器学习算法来说,任何模型预测值和真实值之间的差值要有一个衡量的指标——损失函数(loss function 或 cost function),这个差值可以通过损失函数计算得来的。拿什么做损失函数是可以选择、试验的,如回归问题用
均方根预测rmse:root mean squared error或者 分类问题用Logistic Loss. - 对于每个样本, 通过每颗树预测后可表示为。由于XGboost是一个加法模型,最终预测值可以表示为每颗树的累加之和。
- 对于每个棵树的其复杂度一般是要限制的,如果每棵树过于复杂,就是每个弱分类器过于复杂,极易导致过拟合,机器学习中常用正则项(regularization term)惩罚过于复杂的模型。复杂度表示为,累加后表示为:
这就是XGboost 目标函数基本解释。
2. 如何通过boosting算法学习到的第t棵树?
因为XGboost是boosting算法中一员,可采用前向分步加法来计算,第i个样本的第t步的预测值:
就是,第步预测等于第步预测值加上第t棵树的预测值,其中第步预测值在这时可以看做已知常数。将式4代入式1有:
上式5中,只有是变量。第2步到第3步是因为对于从到时刻,对应树的复杂度由于树已经确定可以看作一个常数,数学表示如下:
3. 泰勒近似XGboost目标函数
对于在处阶导都存在的函数,我们可以用其泰勒展开近似。
根据泰勒公式,在展开为:
那么对于XGboost目标函数, 根据式5,对应损失为。其中,
- 棵树的预测值看成
- 正在训练的看作
而对于式5中, 损失函数对即的一阶偏导和二阶偏导分别可记为,如下式9中表示。
那么损失函数可以改写为:
其中,
将式8代入式5得:
我们可以去掉常数项,这样就有:
这里由式9中表示。
如果使用平方损失,就有:

4. XGboost中的决策树及复杂度
XGboost的基模型不仅支持决策树,还支持线性模型。本文只介绍决策树。其由两部分组成:
- 叶子节点的权重向量
- 每个实例样本到叶子节点的映射关系(其实就是一个树型的分支结构)
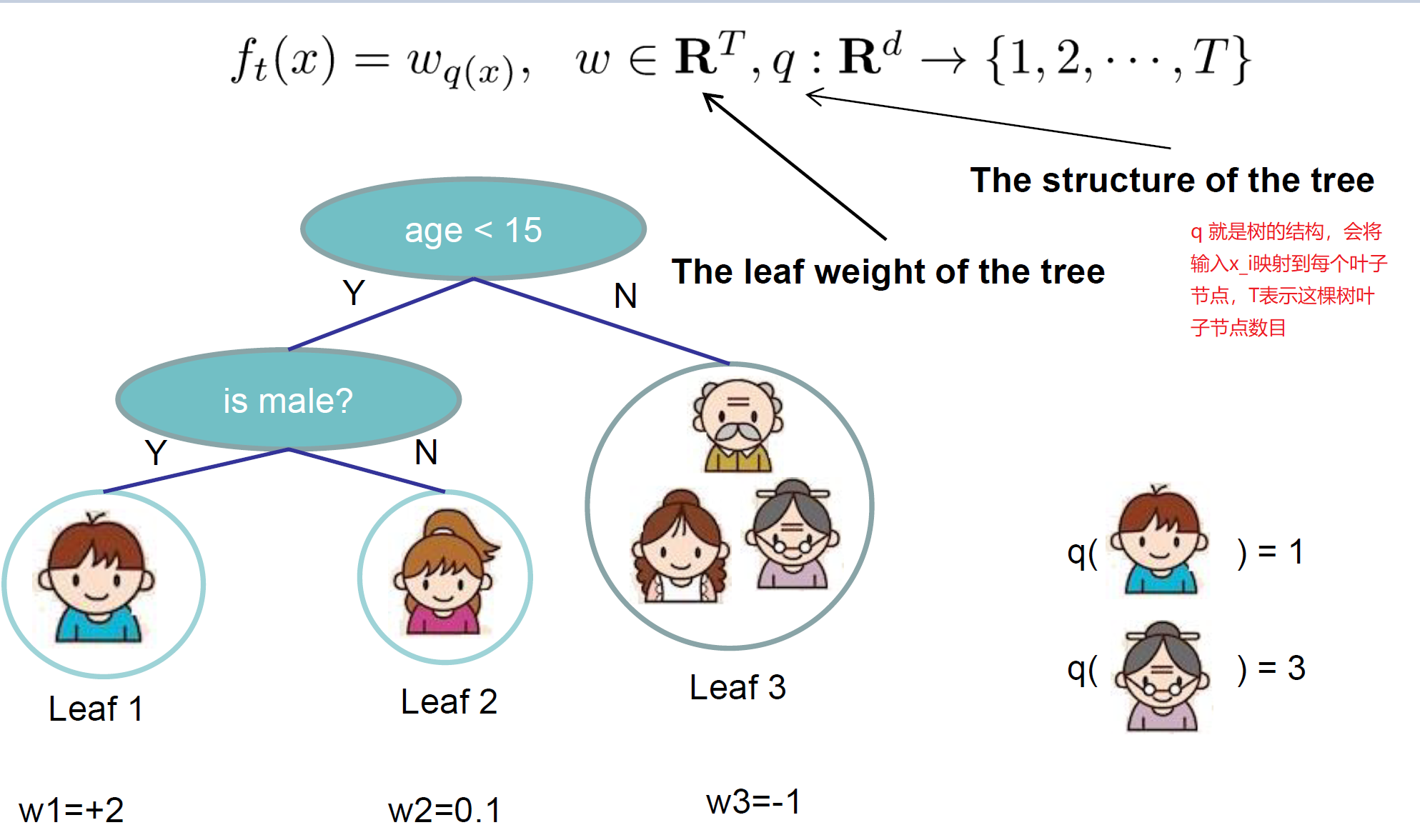
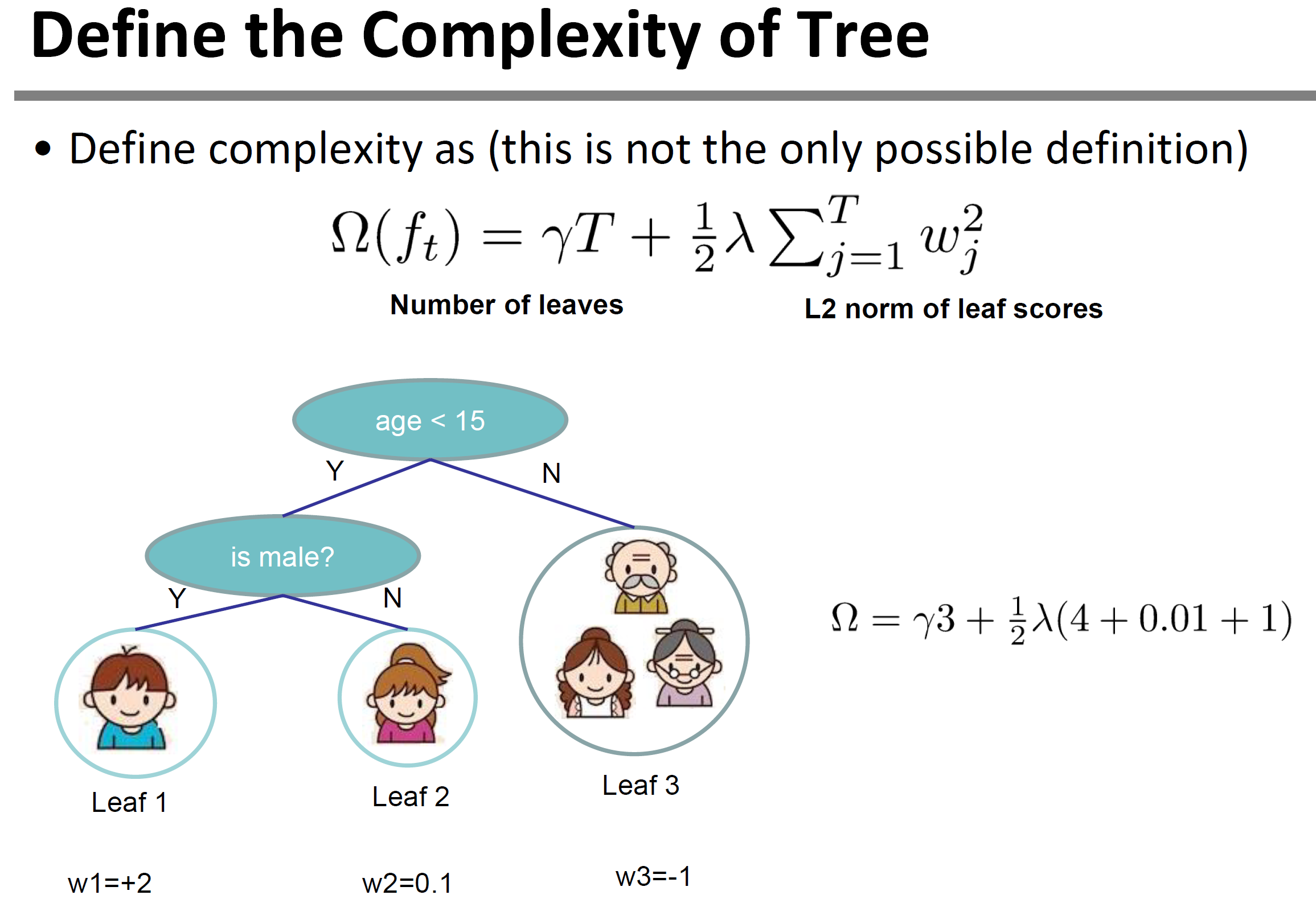
这样我们就可定义决策树的复杂度由叶子节点数目构成,叶子节点越少模型越简单,此外叶子节点也不能权重过大。这样复杂度就可以表示为叶子节点数目和对应权重的范数。具体表示为:
定义树的复杂度图示如下:
5. 叶子节点归组
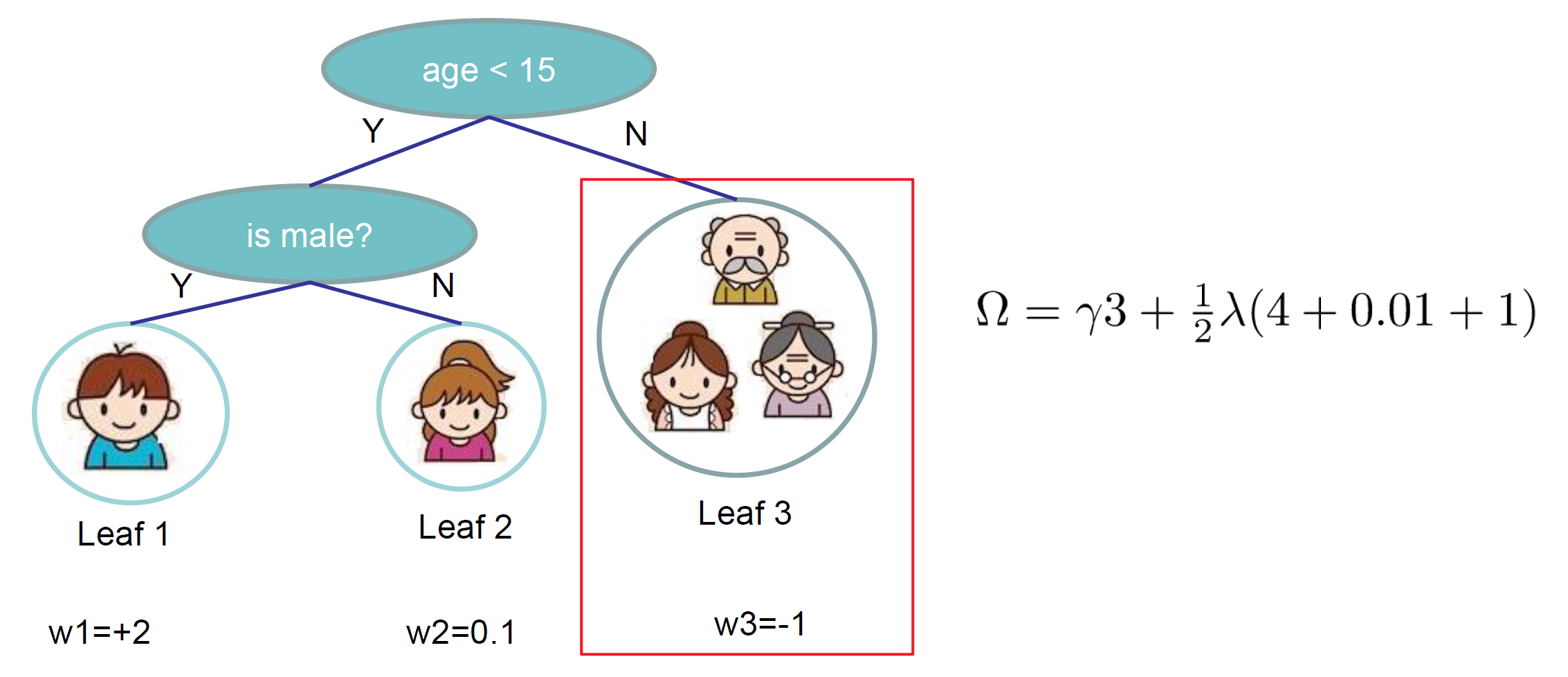
对于上图中叶子节点3,我们可以将其所有样本都划入到一个叶子节点的集合中,假设这个叶子节点为第个,那么可以数学表达为。将式12和13代入式11并结合该表达式有:
上式中,第二步是遍历所有样本之后求每个样本的损失和,但也可从每个叶子节点出发,计算每个叶子节点中样本集合的损失和,这就是 和表达的意思,即划分到每个叶子节点中样本集合的损失和。 表示第 个叶子节点取值。
不妨假定以下记号:
其中,
- : 所有第个叶子节点所包含的一阶偏导数之和,是一个常数。
- : 所有第个叶子节点所包含的二阶偏导数之和,是一个常数。
将式15代入式14可得:
在第步时,是步已经确定的结构,可以计算得到,是常数。因此式16只有叶子节点权重是不确定的。
6. 树结构打分
上小节中,我们已经将目标表达式进一步简化了。现在我们来求其极小值。
不妨回忆一下一元二次函数的极小值求解,假定有如下函数:
易得:
那对于式16,我们只看一个叶子节点有:
记得只将看作变量,那么可得:
代入式19得:
其用来衡量每棵树结构的好坏。代入式16得到整个目标函数为:
下图是目标函数计算例子,我们可以求得目标函数对每个节点中每个样本的一阶偏导数和二阶偏导数,然后对于每个节点中样本集合求, 最后遍历求和决策树的所有节点就得到了目标函数。
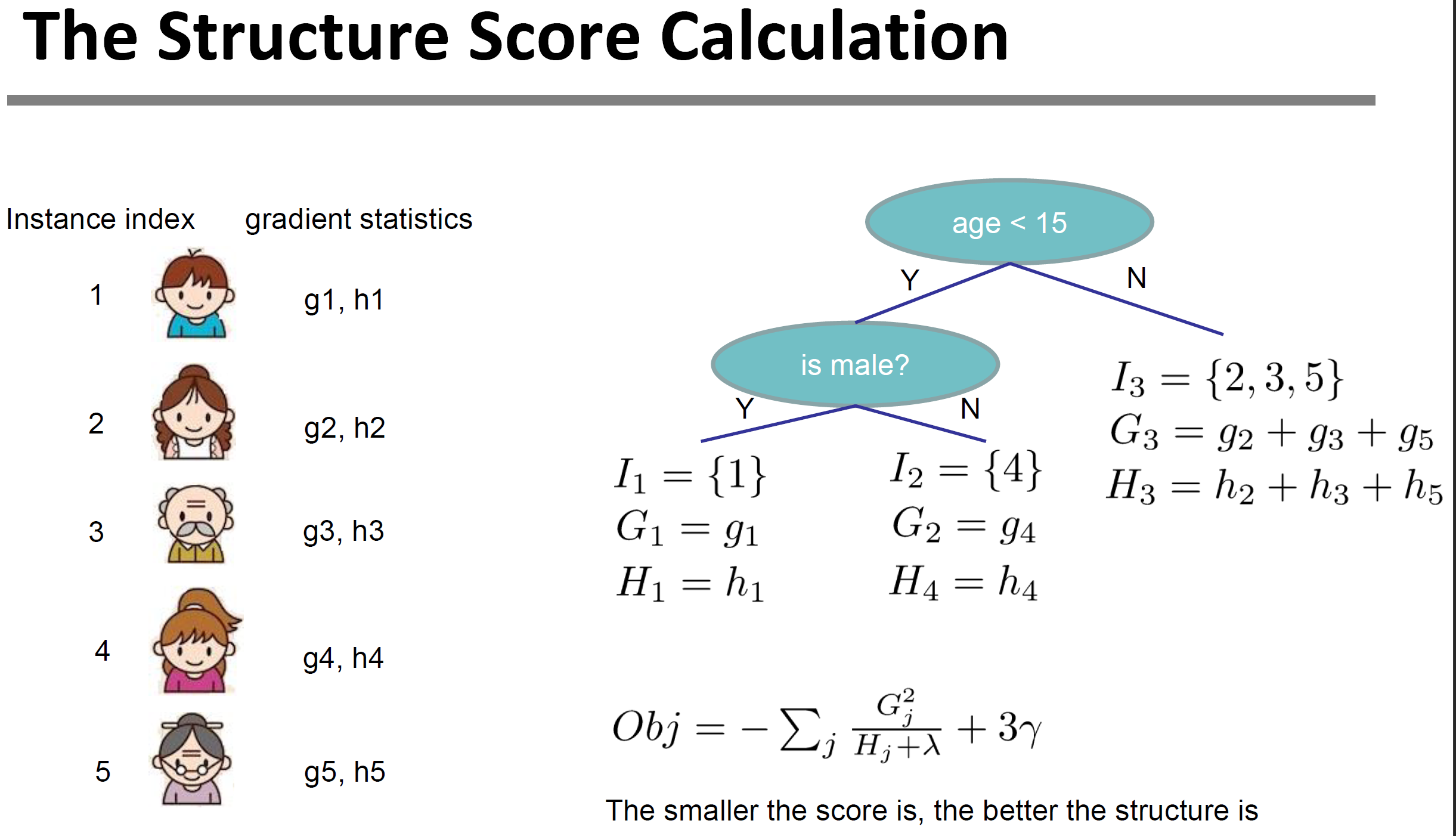
7. 叶子节点最优划分算法
对于单棵树的的搜索算法,我们可以按照以下流程:
- 列举所有可能的树结构q
- 计算对于树结构q的分数
- 找到最佳的树结构,并优化叶子节点权重
但是这样,有可能找到无限棵树结构。在实际训练过程中,建立第t棵树时,最重要的是最优划分叶子节点,XGboost支持两种划分方法——贪心算法和近似算法。
贪心算法
从树的深度为0开始
- 对每个叶子节点尝试进行分裂
- 每次分裂后,原始的叶子节点会分裂为左右两个子叶子节点,原始的叶子节点中样本集将按照划分规则分散到左右两个叶子节点中
- 新分裂完成后,检查这次分裂是否给损失函数带来增益Gain。
这里重点介绍下,分裂增益计算:
根据式22,分裂前,原始叶子节点的目标函数为:
那分裂后,左右叶子节点的目标函数为:
那么带来的增益,式23减去式24得:
注:该特征收益也可作为特征重要性的重要依据。
那么代表着分裂后,目标函数减小了,这样就可以考虑这次分裂结果了。
但是在一个叶子节点分裂时,可能有很多分裂点,每个分裂点都对应一个Gain,如何找到最优的分裂点,我们按照如下步骤来寻找:
- 遍历每个节点的所有特征
- 对于每个特征,按照特征值大小排序
- 线性扫描,找到每个特征的最佳分类特征值
- 在所有特征中找到最好的分裂点,对应分类后Gain最大的特征
整个过程,按照叶子节点特征中最佳分裂特征值来获得分裂后的最佳特征。这就是贪心算法,每次进行分类都遍历全部候选分割点,也叫Global scan。
但当数据量过大导致内存无法一次载入或者在分布式情况下,贪心算法的效率就会变得很低,全局扫描法不再适用。
基于此,XGBoost提出了一系列加快寻找最佳分裂点的方案:
- 特征预排序+缓存:XGBoost在训练之前,预先对每个特征按照特征值大小进行排序,然后保存为block结构,后面的迭代中会重复地使用这个结构,使计算量大大减小。
- 分位点近似法:对每个特征按照特征值排序后,采用类似分位点选取的方式,仅仅选出常数个特征值作为该特征的候选分割点,在寻找该特征的最佳分割点时,从候选分割点中选出最优的一个。
- 并行查找:由于各个特征已预先存储为block结构,XGBoost支持利用多个线程并行地计算每个特征的最佳分割点,这不仅大大提升了结点的分裂速度,也极利于大规模训练集的适应性扩展。
8. 早停和剪枝
在决策树和GBDT中,优化方法常见的有早停和后剪枝post-pruning。XGboost也一样:
- 当新的一次分裂所带来的时,这次分裂会使目标函数增大。计算式25过程中,就很容易明白,不能进行这次分裂。
- 如果树深度过深,非常容易过拟合,所以达到最大树深时,也要停止建树。就是常见超参数:
max_depth - 当新的一次分裂后计算左右两个叶子节点样本权重和。如果任何一个叶子节点的样本权重(计算表达式为式20)低于某一个阈值,也要放弃此次分裂。这就是超参数
min_child_weight,这能防止过拟合。
Inference
[1] XGBoost: A Scalable Tree Boosting System
[2] 深入理解XGBoost
[3] XGBoost超详细推导
[4] xgboost
[5] xgboost_usage


